티스토리 뷰
이 포스트는 Malcolm Barrett 페이지의 글을 번역한 것입니다. (원문: An Introduction to Directed Acyclic Graphs (r-project.org))
An Introduction to Directed Acyclic Graphs
용어 정리: 분야에서마다 같은 개념을 부르는 말이 달라, 여기에서는 역학을 중심으로 함.
교란(confounding)이 생략된 변수 편향(omitted variable bias 혹은 selection bias)를 지칭하기도 하고,
선택 편향 (selection bias)은 종종 변수 선택 편향을 의미하기도 함.
# set theme of all DAGs to `theme_dag()`
library(ggdag)
theme_set(theme_dag())
Directed Acyclic Graphs
DAG는 노드라고 불리는 변수 간 관계에 대한 가정을 보여줌
line이나 edge는 한 노드에서 다른 노드를 이어주는 개념인데,
이 edge들이 방향을 가지고 있어, 그 효과를 가리키는 하나의 화살표로 표현됨.
가령, x가 y에 영향을 준다고 가정하면 다음과 같이 나타낼 수 있음
dagify(y ~ x) %>%
ggdag()
또는 다음과 같이 양방향도 가능함
dagify(y ~~ x) %>%
ggdag()
그러나 이것은 측정되지 않은 두 변수의 원인에 대한 약칭임 (즉, 측정되지 않은 교란, unmeasured confounding)
# canonicalize the DAG: Add the latent variable in to the graph
dagify(y ~~ x) %>%
ggdag_canonical() 
DAG은 비순환(acyclic)적인데, 이는 피드백이 없는 loop이라는 의미이며,
변수는 자손(descendant)을 가질 수 없음. 위의 예는 모두 acyclic이기 때문에 DAG이며, 아래의 예는 DAG가 아님.
dagify(y ~ x, x ~ a, a ~ y) %>%
ggdag() 
Structural Causal Graphs
ggdag은 구조 원인 모델 (structural causal models, SCMs)을 고려함. 즉, 변수 집합에 대한 원인을 보여주는 것.
이는 우리가 직면한 문제의 개념을 넘어, graphical causal path와 통계적 관계 사이의 잘 형성된 링크를 만들어 줌.
Causal DAG는 수학에 기반하고 있지만, 일관적이며 이해하기 쉽기 때문에,
exposure(주: 원인, 독립 변수)와 outcome(주: 결과, 종속 변수) 사이의 인과 효과를 평가할 때, DAG 형태로 그림을 그려보는 것은 그 이면의 수학적 이해를 크게 요구하지 않고 올바른 모델을 고를 수 있게 해 줌.
DAG에 대해 또 달리 생각해 봐야 할 점은, 비모수 구조방정식 (non-parametric structural equation models, SEM)임.
즉, 변수 사이에 명시적으로 경로를 그리지만, DAG의 경우에는 두 변수 사이의 관계가 어떤 형태인지를 고려하지 않고, 방향을 고려함. DAG를 받치는 규칙은 단순한 선이든 복잡한 함수든 상관없이 일정함.
Relationships between variables
흡연과 심장 발작의 관계에 대해 생각해 보자.
흡연이 콜레스테롤에 변화를 일으키고, 이것이 심장 발작의 원인이라고 가정해 볼 수 있음.
smoking_ca_dag <- dagify(cardiacarrest ~ cholesterol,
cholesterol ~ smoking + weight,
smoking ~ unhealthy,
weight ~ unhealthy,
labels = c("cardiacarrest" = "Cardiac\n Arrest", "smoking" = "Smoking",
"cholesterol" = "Cholesterol", "unhealthy" = "Unhealthy\n Lifestyle",
"weight" = "Weight"),
latent = "unhealthy",
exposure = "smoking", outcome = "cardiacarrest")
ggdag(smoking_ca_dag, text = FALSE, use_labels = "label")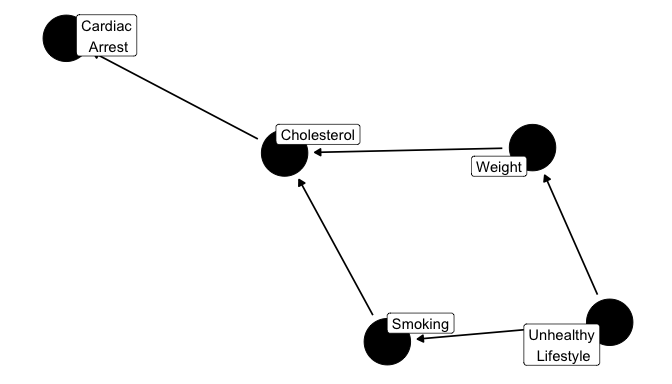
흡연에서 심장 발작에 이르는 경로는 방향성이 있음: 흡연은 콜레스테롤을 높이는데, 이것은 심장 발작의 위험을 증가시킴. 콜레스테롤은 흡연과 심장 발작의 매개변수임. 방향이 있는 경로는 각각이 다음의 원인이 되기 때문에 chain이기도 함.
몸무게도 콜레스테롤을 높인다고 가정하면, 이 또한 심장 발작의 위험도를 높임.
그럼 DAG에 또다른 chain - 몸무게-심장 발작의 새로운 chain이 생기지만, 이 chain은 최소 흡연과 심장 발작 사이의 관계 만큼이나 간접적임. 또한, 흡연자는 과식과 같은 다른 비건강 행동과 연관될 가능성이 좀 더 높음.
DAG에서는 이것이 비건강 생활 습관으로 불리는 잠재된 (비측정) 노드로 표현됨.
비건강한 행동을 좋아하는 것은 흡연과 체증 증가 모두를 야기할 수 있음.
따라서 흡연과 몸무게와의 관계는 chain이라기 보다는 갈라진 경로(forked path)를 통하게 됨 (weight <- unhealthy lifestyle -> smoking), 왜냐하면 그들은 상호 부모격인 비건강 생활습관과 연관되어 있기 때문.
Fork와 chain은 경로의 세가지 주요 타입 중 2개임.
- Chains
- Forks
- Inverted forks (paths with colliders)
두 개의 화살표 머리가 한 노드에서 만날 때, inverted fork라고 함.
두 개 노드의 관계를 기술하는 방법은 많음: parents, children, ancestors, descendants, neighbors.
부모와 자식은 직접적인 관계를 지칭하고, 자손과 조상은 노드에서 경로를 따라가는 어떤 것도 될 수 있음.
이 예에서, 흡연과 몸무게는 둘 다 콜레스테롤의 부모이고, 또한 둘 다 비건강한 생활 습관의 자식임.
심장 발작은 이 그래프에서 모든 노드의 조상이 되는 비건강한 생활 습관의 자손이 됨.
그러면, 흡연이 심장 발작에 인과 효과를 가진다는 연구에서, DAG가 우리를 이끄는 곳은 어딜까?
우리는 단지 흡연에서 심장 발작에 이르는 방향 경로를 알고 싶은 거지만, 간접적이거나 backdoor path 또한 존재함.
이것이 교란(confounding).
causal graph 이론을 가장 발전시킨 Judea Pearl은 교란은 파이프의 물과 같은 거라고 했음: 열린 길로 자유롭게 흐르는 것이고, 우리가 특정 길로 흐르도록 막을 필요가 있는 것. 하나의 경로 이상 막아야(block) 할 지는 몰라도, 똑같은 backdoor path를 따라 많은 지점에서 물을 막을 필요는 없다는 것.
교란에 대해 정말 얘기해야 하는 이유는, 경로를 따라가는 특정 노드보다, 경로에 대한 것이기 때문.
chain과 fork는 열린 통로이기 때문에, DAG에서 아무것도 통제되어 있지 않다면, 어떤 backdoor path도 둘 중 하나여야 함. 심장 발작으로 가는 방향성의 경로 이외에도, 비건강 생활 습관에 있는 forked path를 통하고, 또 거기에서 심장 발작으로의 chain을 통한 열린 backdoor path가 있음.
ggdag_paths(smoking_ca_dag, text = FALSE, use_labels = "label", shadow = TRUE)

이 예제 분석에서 우리는 backdoor path를 설명할 필요가 있음.
이를 설명하는 많은 방법들이 있음 (각 장단점 존재) - stratification, matching, inverse probability weighting.
그러나 각 전략은 어떤 변수들이 설명하는 지에 대한 결정(decision)을 포함해야 함.
많은 분석가들은 모든 가능한 교란인자를 넣는 전략을 택함. 이것이 나쁠 수 있는 이유는 collider나 mediator를 통제(adjust for)하는 것이 편향(bias)을 야기할 수 있기 때문.
대신, 우리는 최소 충분한 adjustment set을 살펴 볼 것: 가령 통제 됐을 때, 모든 backdoor path를 차단하지만 필요 이상으로 포함하거나 제외하지는 않는 공변수 set. 이것은 많은 최소 충분 집합이 있을 수 있음을 의미하며,
만약 주어진 집합에서 하나의 변수를 제거하더라도 backdoor path는 열리게 됨.
가령, x -> y로 가는 첫번째 작은 그림과 같은 DAG는 닫힐(close) backdoor path가 없으므로, 최소 충분 통제 집합(minimally sufficient adjustment set)은 공집합({})이 됨.
또, 순환(cyclic) DAG나 중요 변수가 측정되지 않은 DAG의 경우는 닫힌 backdoor path를 위한 어떤 충분한 집합도 만들어 내지 못함.
흡연 - 심장 발작 문제에서, 하나의 변수를 하진 하나의 집합이 있음: {몸무게}.
몸무게를 고려하는 것은 흡연과 심장 발작 관계의 불편추정(unbiased estimate)을 제공할 수 있음 (이 DAG가 맞다는 가정하에). 그러나 흡연과 심장 발작 사이에 중개하는 변수이기 때문에, 콜레스테롤을 통제할 필요는 없음; 콜레스테롤을 통제하는 것은 그 둘을 차단한다는 의미이고, 이것은 이 추정을 편향되게 하기 때문.
ggdag_adjustment_set(smoking_ca_dag, text = FALSE, use_labels = "label", shadow = TRUE)
좀 더 복잡한 DAG는 더 복잡한 통제 집합(adjustment set)을 만들어 냄; 해당 DAG가 맞다는 가정 하에, 어떤 주어진 집합도 이론적으로는 결과(outcome)와 원인(exposure) 사이의 backdoor path를 닫음. 또한, 데이터에 따라서 하나의 집합은 다른 것 보다 사용하기에 더 좋을 수도 있음.
가령, 하나의 집합은 많은 결측치를 가지거나 측정 에러를 가졌다고 알려진 변수를 포함할 수 있고, 그것은 포함할 필요가 있는 변수를 더 잘 표현할 거라고 생각하는 집합을 사용하는게 더 나을 수 있다는 것일 수도 있음. 노드를 실제로 잘 표현하지 않는 변수를 포함하는 것은 잔차 교란(residual confounding)이 될 수도 있음.
backdoor path를 따라가는 다중 변수나 어떤 backdoor path도 따르지 않는 변수를 통제하는 것은 어떨까?
그러한 변수들은 collider나 mediator가 아니라고 해도, 모델에 따라 여러 문제를 만들 수 있음.
risk ratio와 같은 어떤 추정은 교란 변수가 없을 때(non-confounder)는 작동을 잘 하는데, 이는 그들이 collapsible 하기 때문: risk ratio는 non-confounder의 층위에서는 상수임(일정).
odds ratio나 hazard ratio와 같은 추정은 non-collapsible 함: 이는 non-confounder의 층위에서 꼭 상수인 것은 아니기 때문에 포함 여부에 따라 편향이 발생될 수 있는데,
종속 변수가 집단에서 희귀한 경우(희귀 질병 등)라거나 incident-density sampling과 같은 정교한 샘플링 기술을 사용할 때, risk ratio를 근사할 때와 같은 특정 상황들이 있음. 그렇지 않고 추가적인 변수를 포함하는 것은 문제가 될 수 있음.
Colliders and collider-stratification bias
x -> m <- y인 inverted folk에서, 2개 이상의 화살 머리가 만나는 노드를 collider라고 함.
inverted folk는 collider에 의해 block되어 있기 때문에 열린 경로가 아님. 즉, x -> y의 인과 효과를 설명하기 위해 m을 고려할 필요가 없음 (backdoor path가 이미 m에 의해 block되어 있기 때문)
예를 들어, 독감과 수두는 독립적이지만 (각각의 원인 바이러스가 다르고 서로 관련이 없음), 현실에서는 그들을 연결시키는 confounder가 있지만(면역 체계 저하 등), 이 예제에서는 교란 변수가 없다고 가정하겠음 (unconfounded).
그러나 독감과 수두는 모두 '열'을 일으킴. 따라서 DAG는 아래와 같음.
fever_dag <- collider_triangle(x = "Influenza", y = "Chicken Pox", m = "Fever")
ggdag(fever_dag, text = FALSE, use_labels = "label")
만약 수두에 대한 독감의 인과 효과를 평가하고 싶다면, 어떤 것에 대해서도 설명할(account for) 필요가 없음.
Pearl에 의해 사용된 용어에 의하면, 그것들은 각자에게 효과도 없을 뿐더러 backdoor path도 없기 때문에 이미 d-seperated (direction separated)되어 있는 것.
ggdag_dseparated(fever_dag, text = FALSE, use_labels = "label")
그러나, '열'을 통제한다면, 그것들은 collider (열) 층위 내에서 연관됨. 그 둘 사이에 편향적인 경로(biasing pathway)를 열면 d-connected 됨.
ggdag_dseparated(fever_dag, controlling_for = "m", text = FALSE, use_labels = "label")
이것은 처음엔 반직관적으로 보임. 왜 교란 변수를 통제하는 것은 편향은 줄이는데, collider를 통제하는(adjusting) 하는 것은 편향을 증가시키는가?
이는 열이 열이 나는가 나지 않는가가 질병에 대해 뭔가를 말해주기 때문임. 즉, 만약 열이 나는데, 독감은 아니라면, 수두를 앓고 있다는 근거.
Pearl은 그것을 대수로 표현했는데, y = 10 + m이라고 했을 때, m=1이라는 걸 알면 y도 알 수 있음.
불행하게도 덜 명백한 두번째 collider-stratification bias의 형태가 있는데, 이는 collider의 자손에 대해 통제(adjust)하는 것임. 즉, collider에서 파생되어 내려오는 변수는 이런 형태의 편향을 일으킬 수 있음.
가령, 독감-수두 예제에서, 열이 난다는 것은 사람들이 해열제를 먹게 만드는데, 해열제는 열의 하위에 있기 때문에, 그것을 통제하는 것은 downstream collider-stratification bias를 만들어 냄.
dagify(fever ~ flu + pox, acetaminophen ~ fever,
labels = c("flu" = "Influenza",
"pox" = "Chicken Pox", "fever" = "Fever", "acetaminophen" = "Acetaminophen")) %>%
ggdag_dseparated(from = "flu", to = "pox", controlling_for = "acetaminophen",
text = FALSE, use_labels = "label")
collider-stratification bias는 많은 유형의 편향에 책임이 있고(영향을 주고), 적절히 다뤄지지 못함.
Selection bias, missing data, and publication bias 들이 이러한 collider-stratification bias로 여겨지며,
좀 더 복잡한 DAG에서는 두꺼워 질 수 있음; 때로 colldier는 confounder가 되기도 하므로, collider를 통제하는 것으로부터 남는 편향(bias)을 통제하는 전략을 생각하거나, 최소한의 편향이 결과로 남도록 전략을 고를 필요도 있음.
(다음 참고: common structures of bias )
Mediation
매개 변수를 통제하는 것 또한 편향을 야기할 수 있는데, 이는 y에 대한 x의 총효과를 부분으로 해체하기 때문임.
연구 문제에 따라 그것이 원하는 부분일 수도 있음 (이런 경우 SEM과 같은 매개 분석을 사용해서 직접, 간접, 총효과를 추정하게 됨).
흡연 예제로 다시 돌아가면, 흡연이 심장 발작에 얼마나 영향을 주는지만 신경을 썼지, 콜레스테롤을 통한 경로는 고려하지 않았음. 게다가 (이 DAG에서는) 콜레스테롤이 흡연에서 심장 발작으로 가는 유일한 방향 경로를 간섭(intercept)했기 때문에, 그것을 통제하는 것이 이 관계를 차단하는 것이었음 (흡연과 심장 발작은 관련이 없다고 나올 것 - 그래프에서 collider를 통제함으로써 열린 경로를 포함하지 않았음)
ggdag_dseparated(smoking_ca_dag, controlling_for = c("weight", "cholesterol"),
text = FALSE, use_labels = "label", collider_lines = FALSE)
이제 흡연과 심장 발작은 d-seperated됨.
우리의 질문은 흡연이 심장 발작에 주는 총효과였기 때문에, 이 결과는 편향적이 될 것임.
Resources
- Judea Pearl also has a number of texts on the subject of varying technical difficulty. A friendly start is his recently released Book of Why, as well as his article summarizing the book: The Seven Tools of Causal Inference with Reflections on Machine Learning. A more technical introduction is Causal Inference in Statistics: A Primer. See also his article with Sander Greenland and James Robins on collapsibility: Confounding and Collapsibility in Causal Inference.
- Miguel Hernán, who has written extensively on the subject of causal inference and DAGs, has an accessible course on edx that teaches the use of DAGs for causal inference: Causal Diagrams: Draw Your Assumptions Before Your Conclusions. Also see his article The Hazard of Hazard Ratios for more on issues with hazard ratios in causal inference.
- Julia Rohrer has a very readable paper introducing DAGs, mostly from the perspective of psychology: Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data
- If you’re an epidemiologist, I also recommend the chapter on DAGs in Modern Epidemiology.
- Total
- Today
- Yesterday
- ECG
- featuremap
- 생존곡선
- GPU설치
- vcf
- HRV
- missing_value
- sequenced data
- cnn
- 그룹비교
- 평균분석
- sounddevice
- 생존분석
- r
- pre-train
- rgb2gray
- fasta
- gray2rgb
- 실험통계
- plink
- 딥러닝
- Bioinfo
- PTB
- 인공지능
- GradCam
- 생존함수
- NGS
- pmm
- psychopy
- SNP
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
