티스토리 뷰
- 생존 함수 비교
두 그룹의 생존 함수의 동일성 여부를 검정하기 위한 방법
- 귀무 가설 H0: S1(t) = S2(t)
- 대립 가설은 두 가지
1) H1: S1(t) > S2(t) 또는 H1: S2(t) < S2(t)
(모든 시간에 걸쳐 한 그룹의 생존 함수가 다른 그룹보다 크거가 작음)
2) t > a 일 때, H1:S1(t) > S2(t)이고, t ≤ a 일 때, H1: S1(t) ≤ S2(t)
(a라는 특정 시점을 기준으로 두 그룹의 생존 함수가 교차되는 경우)
- 로그 순위 검정 (Log-Rank Test)
두 그룹의 생존 함수의 동질성 검정
각 사건 발생 시점 t(i)에서 그룹 1에 대해 귀무가설과 대립 가설 하에서 구한 위험률의 추정량 사용
t(i) 시점에서 관찰된 위험률은 O(1t) / N(1t)

귀무 가설이 맞다면 위험률은 비슷한 값을 가질 것
t(i) 시점에서 그룹1의 관측된 사건 수(O(1t))와 귀무 가설 하에서 구한 d(1t)의 기대사건 수 E(1t)의 차이의 합으로 검정 통계량을 구하면 다음과 같음

(이는 범주형 자료의 카이 제곱 검정과 비슷)
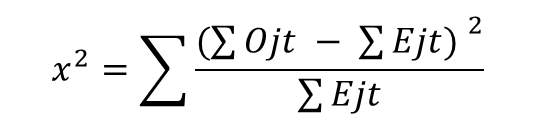
예제 1) 다음 두 그룹의 동질성 검정을 해보자 (df=1, α = 0.05일 때 기각값=3.84)
| Time | N1t (risk) | N2t (risk) | Nt (total risk) | O1t (event) | O2t (event) | Ot (total event) | E1t (expt. evt) | E2t (expt. evt) |
| 8 | 10 | 10 | 20 | 1 | 0 | 1 | 0.500 | 0.500 |
| 12 | 8 | 10 | 18 | 1 | 0 | 1 | 0.444 | 0.556 |
| 14 | 7 | 10 | 17 | 1 | 0 | 1 | 0.412 | 0.588 |
| 21 | 5 | 10 | 15 | 1 | 0 | 1 | 0.333 | 0.667 |
| 26 | 4 | 8 | 12 | 1 | 0 | 1 | 0.333 | 0.667 |
| 27 | 3 | 8 | 11 | 1 | 0 | 1 | 0.273 | 0.727 |
| 28 | 2 | 8 | 10 | 0 | 1 | 1 | 0.200 | 0.800 |
| 33 | 1 | 7 | 8 | 0 | 1 | 1 | 0.125 | 0.875 |
| 41 | 0 | 5 | 5 | 0 | 1 | 1 | 0.000 | 1.000 |
| sum | 6 | 3 | 2.620 | 6.380 |

→ 6.151 > 3.84 이므로, 귀무가설 기각
예제 2) 생존 곡선 비교
library(survival)
library(IswR)
head(melanom)
# Surv(time, event): the followup time with status indicator
attach(melanom)
head(Surv(days, status==1))

- status: 0 dead, 1 alive, 2 others
- days: observation time
- ulc: 1 present, 2 absent
- +: censored observation (10+: not died in 10 days, 35+: alive, 185: died)
- Kaplan-Meier Curve
event 발생 시점마다 생존율 계산
관찰 기간 순서대로 자료 정리 후, 각 구간 별로 관찰 대상 수 중 생존자 수로 구간 생존율 및 누적 생존율 계산
surv.bysex <- survfit(Surv(days, status==1) ~ sex)
summary(surv.bysex)
plot(surv.bysex)
plot(surv.bysex, conf.int=TRUE, col=c("red", "blue")
- 로그 순위 검정
H0: 두 그룹의 생존 곡선은 같다
H1: 두 그룹의 생존 곡선은 같지 않다
survdiff(Surv(days, status==1)~sex)
P value < 0.05 이므로 (0.01) 귀무 가설을 기각
예제 3) R에서 데이터 생성하여 Kaplan-Meier 곡선을 그리고 로그 순위 검정
# Group 벡터 생성
Chemo.Group <- c(rep(1,10),rep(2,10))
# Status 벡터 생성
Chemo.Status <- c(rep(1,6),rep(0,4),rep(0,7),rep(1,3))
# 시간 벡터 생성
Time.Month <- c(8, 12, 14, 21, 26, 27, 8, 14, 28, 33, 21, 21, 33, rep(41, 4), 28, 33, 41)
# 위 벡터를 데이터프레임으로 병합
Chemo.data <- data.frame(Time.Month, Chemo.Status, Chemo.Group)
# 서바이벌 데이터 확인
Surv(Time.Month, Chemo.Status)
Chemo.diff <- survdiff(Surv(Time.Month, Chemo.Status) ~ Chemo.Group, data=Chemo.data)



# Kaplan-Meier curv
Chemo.plot <- survfit(Surv(Time.Month, Chemo.Status) ~ Chemo.Group, data=Chemo.data)
summary(Chemo.plot)
Chemo.diff <- survdiff(Surv(Time.Month, Chemo.Status) ~ Chemo.Group, data=Chemo.data)
plot(Chemo.plot, xlab='Time', ylab='% Surviving', col=c('red','blue'),
main='Survival Chemotherapy (n=20)')
legend('bottomleft', legend=c('Group1', 'Group2'), lty=c(1,1), col=c('red', 'blue'))
- 가중 로그 순위 검정
- 위 예제는 모든 시간대에 동일한 가중치(1)를 부여했으나, 실제 자료 분석 시 두 생존 함수 차이가 초반에 두드러지는 경우, 이러한 차이를 부각시키기 위해 초반에 큰 가중치를 주면 검정력을 높일 수 있음
- 관심 시간 대에 더 많은 가중치를 부여하는 것을 가중 로그 순위 검정(Weighted log-rank test)이라고 함
- 다양한 방법이 있으나 Survfit에서는 Wn(t) = Yn(t)^p로 계산함 (Wn(t): 가중치, Yn(t)^p: number at risk)
Survfit 함수에서는 rho가 P의 역할을 하며, 초기값은 0
- p = 1일 때는 Peto-Peto Gehan-Wilcoxon test를 시행 (앞으로 갈수록 가중치)
- p = -1일 때는 뒤로 갈수록 가중치를 줌
survdiff(Surv(Time.Month, Chemo.Status) ~ Chemo.Group, data=Chemo.data, rho=-1)
survdiff(Surv(Time.Month, Chemo.Status) ~ Chemo.Group, data=Chemo.data, rho=1)
survdiff(Surv(Time.Month, Chemo.Status) ~ Chemo.Group, data=Chemo.data, rho=0)
---> 가중치에 따라 P값이 달라짐을 확인할 수 있음
'데이터 분석 > 확률 통계' 카테고리의 다른 글
| 생존 분석 5 (TCGA cases) (0) | 2023.01.05 |
|---|---|
| 생존 분석 4 (Cox proportional hazards model) (1) | 2023.01.05 |
| 생존 분석 2 (Kaplan-Meier estimation) (0) | 2023.01.05 |
| 생존 분석 1 (생존 함수 추정) (0) | 2023.01.04 |
| 다중회귀에서 상관 관계와 억제 효과 (0) | 2023.01.04 |
- Total
- Today
- Yesterday
- pre-train
- GradCam
- 인공지능
- vcf
- ECG
- 평균분석
- NGS
- psychopy
- cnn
- Bioinfo
- 실험통계
- SNP
- 생존함수
- 딥러닝
- gray2rgb
- r
- 생존분석
- HRV
- 생존곡선
- sounddevice
- pmm
- PTB
- missing_value
- rgb2gray
- fasta
- GPU설치
- plink
- 그룹비교
- sequenced data
- featuremap
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
